用Python从头实现一个神经网络来理解神经网络的原理4

***14 ***代码：一个完整的神经网络

我们终于可以实现一个完整的神经网络了：

import numpy as np
defsigmoid(x):# Sigmoid activation function: f(x) = 1 / (1 + e^(-x))  return 1 / (1 + np.exp(-x))
defderiv_sigmoid(x):  # Derivative of sigmoid: f'(x) = f(x) * (1 - f(x))  fx = sigmoid(x)  return fx * (1 - fx)
defmse_loss(y_true, y_pred):  # y_true和y_pred是相同长度的numpy数组。  return ((y_true - y_pred) ** 2).mean()
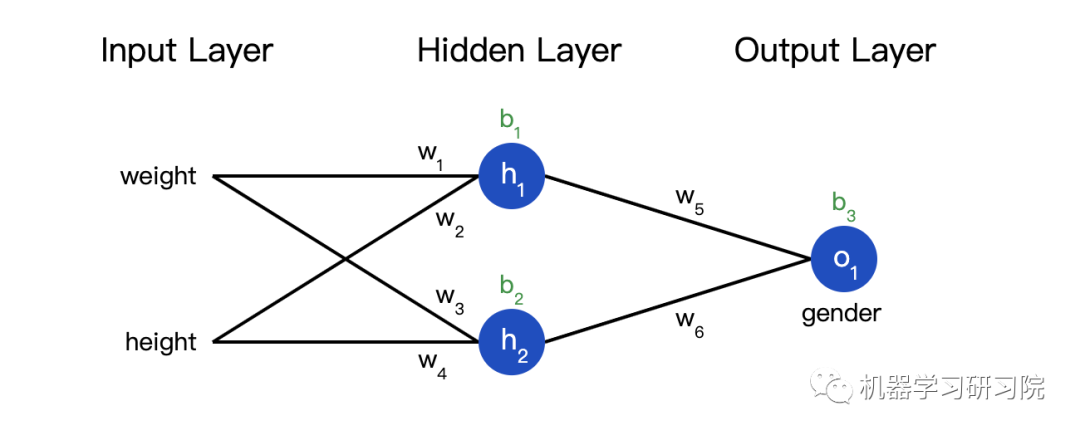
classOurNeuralNetwork:  '''  A neural network with:    - 2 inputs    - a hidden layer with 2 neurons (h1, h2)    - an output layer with 1 neuron (o1)
  *** 免责声明 ***:    下面的代码是为了简单和演示，而不是最佳的。    真正的神经网络代码与此完全不同。不要使用此代码。    相反，读/运行它来理解这个特定的网络是如何工作的。  '''  def__init__(self):    # 权重，Weights    self.w1 = np.random.normal()    self.w2 = np.random.normal()    self.w3 = np.random.normal()    self.w4 = np.random.normal()    self.w5 = np.random.normal()    self.w6 = np.random.normal()
    # 截距项，Biases    self.b1 = np.random.normal()    self.b2 = np.random.normal()    self.b3 = np.random.normal()
  deffeedforward(self, x):    # X是一个有2个元素的数字数组。    h1 = sigmoid(self.w1 * x[0] + self.w2 * x[1] + self.b1)    h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2)    o1 = sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3)    return o1
  deftrain(self, data, all_y_trues):    '''    - data is a (n x 2) numpy array, n = # of samples in the dataset.    - all_y_trues is a numpy array with n elements.      Elements in all_y_trues correspond to those in data.    '''    learn_rate = 0.1    epochs = 1000 # 遍历整个数据集的次数
    for epoch in range(epochs):      for x, y_true in zip(data, all_y_trues):        # --- 做一个前馈(稍后我们将需要这些值)        sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1        h1 = sigmoid(sum_h1)
        sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2        h2 = sigmoid(sum_h2)
        sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3        o1 = sigmoid(sum_o1)        y_pred = o1
        # --- 计算偏导数。        # --- Naming: d_L_d_w1 represents "partial L / partial w1"        d_L_d_ypred = -2 * (y_true - y_pred)
        # Neuron o1        d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1)        d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1)        d_ypred_d_b3 = deriv_sigmoid(sum_o1)
        d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1)        d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1)
        # Neuron h1        d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1)        d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1)        d_h1_d_b1 = deriv_sigmoid(sum_h1)
        # Neuron h2        d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2)        d_h2_d_w4 = x[1] * deriv_sigmoid(sum_h2)        d_h2_d_b2 = deriv_sigmoid(sum_h2)
        # --- 更新权重和偏差        # Neuron h1        self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1        self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2        self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1
        # Neuron h2        self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3        self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4        self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2
        # Neuron o1        self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5        self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6        self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3
      # --- 在每次epoch结束时计算总损失       if epoch % 10 == 0:        y_preds = np.apply_along_axis(self.feedforward, 1, data)        loss = mse_loss(all_y_trues, y_preds)        print("Epoch %d loss: %.3f" % (epoch, loss))
# 定义数据集data = np.array([  [-2, -1],  # Alice  [25, 6],   # Bob  [17, 4],   # Charlie  [-15, -6], # Diana])all_y_trues = np.array([  1, # Alice  0, # Bob  0, # Charlie  1, # Diana])
# 训练我们的神经网络!network = OurNeuralNetwork()network.train(data, all_y_trues)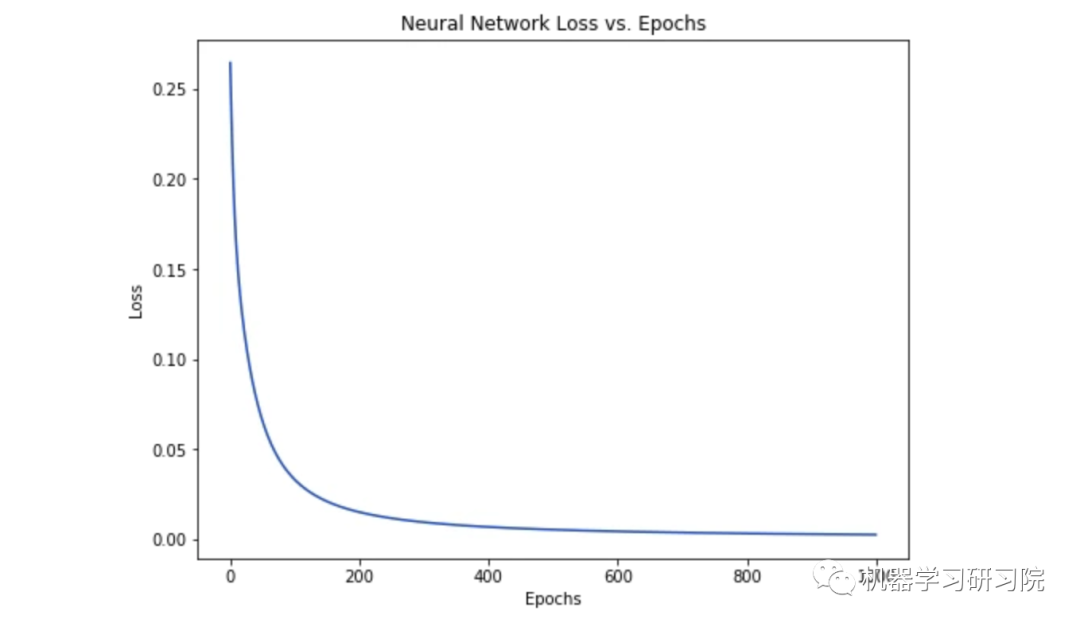

现在我们可以用这个网络来预测性别了：

# 做一些预测emily = np.array([-7, -3]) # 128 磅, 63 英寸frank = np.array([20, 2])  # 155 磅, 68 英寸print("Emily: %.3f" % network.feedforward(emily)) # 0.951 - Fprint("Frank: %.3f" % network.feedforward(frank)) # 0.039 - M

*15 ***** 接下来？

搞定了一个简单的神经网络，快速回顾一下：

• 介绍了神经网络的基本结构——神经元；
• 在神经元中使用S型激活函数；
• 神经网络就是连接在一起的神经元；
• 构建了一个数据集，输入（或特征）是体重和身高，输出（或标签）是性别；
• 学习了损失函数和均方差损失；
• 训练网络就是最小化其损失；
• 用反向传播方法计算偏导；
• 用随机梯度下降法训练网络；

接下来你还可以：

• 用机器学习库实现更大更好的神经网络，例如TensorFlow、Keras和PyTorch；
• 其他类型的激活函数；
• 其他类型的优化器；
• 学习卷积神经网络，这给计算机视觉领域带来了革命；
• 学习递归神经网络，常用于自然语言处理；